Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 |
Tags
- Web Server
- 비주얼스튜디오
- 루즈 커플링
- 시간빼기
- 숫자 포맷
- c#
- 근의공식
- 웹서버 만들기
- 문자열 포맷
- 프로그래밍
- migration
- 브로드캐스트
- swagger
- 구독패턴
- c# 시간계산
- c샵
- default
- http server
- 2차방정식
- microsoft.entityframeworkcore.design
- 데이터관리
- loose coupling
- cshop
- 개발
- c# 포맷
- 날짜 포맷
- 시간더하기
- 이벤트 기반 아키텍처
- Visual Studio
- timespan
Archives
- Today
- Total
Debug & Think
[C#] 2차방정식 풀기: 근의 공식 활용 본문
최근 코딩 테스트 문제를 풀다가 학창 시절 배운 2차 방정식이 생각보다 실생활 문제 해결에도 쓰인다는 걸 깨달아 흥미로웠습니다. 이번 글에서는 그 경험과 함께 C#을 활용해 어떻게 접근했는지를 소개합니다.
📖 문제 상황 (창작 예시)
한 마을 축제에서 거대한 종이학이 날아올라 멋지게 펼쳐진 뒤 K개의 중간 종이학으로 나뉘고,
각 중간 종이학은 다시 K개의 작은 종이학으로 접혀 완성됩니다.
이후에는 더 이상 종이학이 생기지 않습니다.
이때 만들어진 모든 종이학의 수가 result라면, 과연 K는 몇일까?
🔍 수식으로 분석해보기
- 큰 종이학: 1개
- 중간 종이학: K개
- 작은 종이학: K * K개
📐 전체 종이학 수:
result = 1 + K + K²
이 식을 정리하면 다음과 같은 2차 방정식이 됩니다:
K² + K + 1 = result
→ K² + K + (1 - result) = 0
💡 2차 방정식으로 K 구하기
이제 C#으로 result를 입력받고, 가능한 정수 해 K를 구하는 코드를 작성
1️⃣ 판별식 선언
//k² + k + (1 - result) = 0 형태
//⬇
//ak² + bk + c = 0
int a = 1;
int b = 1;
int c = 1 - result;
// discriminant 뜻 : 판별식
double discriminant = b * b - 4 * a * c; // discriminant는 (b² - 4ac)2️⃣ 제곱근
double sqrtDiscriminant = Math.Sqrt(discriminant);- Math.Sqrt()
→ 제곱근(sqrt)을 구하는 함수
ex) Math.Sqrt(9) → 3
항상 double 타입의 실수 값을 반환 - discriminant : 판별식
→ 이차방정식의 판별식. D = b² - 4ac
D 값이
• > 0보다 크면 실수 두 개 - 현재 필요한 값
• = 0이면 중근 (하나의 값)
• < 0보다 작으면 허근 (실수 해 없음) - sqrtDiscriminant
→ 판별식" b² - 4ac의 제곱근" 이라는 의미의 변수입니다.
제곱근을 활용하는 이유는
근의 공식 x = (-b ± √(b² - 4ac)) / 2a 에서 √(b² - 4ac)의 루트를 없애기 위해 필요
// 예제
int a = 1, b = 1, c = -20;
double discriminant = b * b - 4 * a * c; // 1*1 - 4*1*(-20) = 81
double sqrtDiscriminant = Math.Sqrt(discriminant); // sqrt(81) = 9
3️⃣ 정수 확인
if (sqrtDiscriminant % 1 != 0)
- % 1은 소수점 이하 값만 남깁니다.
- 이 식에서 원하는 건 정수 k입니다.
- sqrtDiscriminant % 1 != 0은 "소수점 이하가 0이 아니라면 → 정수가 아니다"는 뜻이기에
정수인지 확인합니다.
4️⃣ 근의 공식 활용
double k1 = (-b + sqrtDiscriminant) / (2 * a);
double k2 = (-b - sqrtDiscriminant) / (2 * a);- 표준적인 이차방정식 형태 ax² + bx + c = 0 에서 값을 구하려면
- 근의 공식 x = (-b ± √(b² - 4ac)) / 2a 을 사용
📌 요약
double discriminant = b * b - 4 * a * c;
double sqrtDiscriminant = Math.Sqrt(discriminant);
double k1 = (-b + sqrtDiscriminant) / (2 * a);
double k2 = (-b - sqrtDiscriminant) / (2 * a);
- 이차방정식의 해를 수학적으로 계산하는 공식을 통해 값을 구하고
k1, k2 중에 정수인 값만 채택하여 k로 사용
수학 공식으로 표현해보면
🎯 목표 식:
1 + k(1 + k) = result① 식 정리:
1 + k(1 + k) = result
=> 1 + k + k² = result
=> k² + k + 1 - result = 0② 이차방정식 형태로 만들기:
k² + k + (1 - result) = 0
⬇
ak² + bk + c = 0
a = 1, b = 1, c = 1 - result③ 근의 공식 사용:
x = (−b ± √(b² − 4ac)) / (2a)
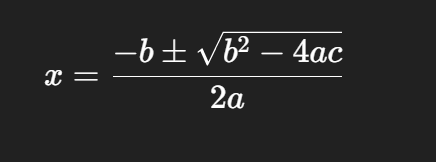
④ 우리 식에 대입:

🧮 전체코드
using System;
class Program
{
static void Main()
{
int result = 21; // 총 종이학 수 (예: 21)
// k² + k + (1 - result) = 0 형태
int a = 1;
int b = 1;
int c = 1 - result;
// discriminant 뜻 : 판별식
double discriminant = b * b - 4 * a * c; // discriminant는 (b² - 4ac)
if (discriminant < 0) // 정수인지 아닌지 판별하는 코드
{
Console.WriteLine("실수 해가 없습니다.");
return;
}
double sqrtDiscriminant = Math.Sqrt(discriminant); // (b² - 4ac)의 제곱근. 루트풀기 위해
if (sqrtDiscriminant % 1 != 0) // % 1는 소수점 이하 값만 남김
{
Console.WriteLine("정수 값이 없습니다.");
return;
}
// 근의 공식 활용
double k1 = (-b + sqrtDiscriminant) / (2 * a);
double k2 = (-b - sqrtDiscriminant) / (2 * a);
// 정수 값만 출력. % 1는 소수점 이하 값만 남김
if (k1 % 1 == 0 && k1 >= 0)
Console.WriteLine($"가능한 K 값: {k1}");
if (k2 % 1 == 0 && k2 != k1 && k2 >= 0)
Console.WriteLine($"가능한 K 값: {k2}");
}
}
